Curiosidades Matemáticas
+22
Monalisa
Atomic Boy
Paranhos
Gigaview
Aleister Crowley
Conde de Monte Cristo
Illuminatus
Legolas
Freud explica
Mr. Enigma
007
Infinito
Geômetra
Maçom 33° Grau
Marley
Homem Vitruviano
Professor Black
Tom Severo
Flautista de Hamelin
Bibi
sombriobyte
Alquimista
26 participantes
Página 1 de 7
Página 1 de 7 • 1, 2, 3, 4, 5, 6, 7 
 Curiosidades Matemáticas
Curiosidades Matemáticas
O matemático Alex Bellos escreveu um artigo muito legal no DailyMail sobre como nós seres humanos temos dificuldade de entender a aleatoriedade e como cometemos grandes erros por isso.
Muitos eventos do nosso dia-a-dia são simplesmente fruto do acaso, mas nós tentamos sempre enxergar algum padrão para explicá-los. Em outras palavras, nós concluímos muitas coisas de forma errada porque queremos dar explicação para tudo.
Um exemplo disso é quando o Ipod surgiu e, na opção de tocar músicas aleatoriamente, as pessoas diziam que o aparelho não funcionava direito porque com frequência as músicas repetiam antes mesmo de tocar outras que ainda não haviam sido tocadas. Parece intuitivo que todas as músicas devam ser tocadas antes que uma mesma música se repita duas ou três vezes. Mas estatisticamente é bastante provável que uma música se repita antes de tocar todas.
Foi aí que o Steve Jobs teve que alterar a configuração do aparelho para agradar os clientes. “Nós o fizemos menos aleatório para parecer mais aleatório”, disse.
Outro exemplo é a Falácia do Apostador ou Falácia de Monte Carlo. Monte Carlo é um cassino, e em 1913 a roleta caiu 26 vezes seguida na cor preta. Os apostadores perderam muito dinheiro apostando no vermelho, pois conforme a sequência de vezes que a roleta caia no preto aumentava, intuitivamente as pessoas acreditavam que haveria uma sequência igualmente grande de vezes que cairia no vermelho. Mas acontece que os eventos são independentes, portanto mesmo tendo caído 25 vezes no preto, a chance da 26ª cair no preto ainda era 50%. E, de fato, caiu.
A moral da história é que alguns eventos peculiares podem, a princípio, parecer ter algum padrão, mas na verdade são aleatórios. Mas então, o que é a aleatoriedade?
É uma coisa bastante difícil de definir. Até os dicionários apresentam definições vagas e distintas. Mas, na verdade, a aleatoriedade é uma palavra que usamos para descrever eventos cuja causa nós desconhecemos e por isso PARECEM ser fruto do acaso. A aleatoriedade pura, na verdade, não existe.
http://bravos.poutz.com/?p=481
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
O número 73
73 é o 21° número primo.
O seu inverso, o número 37, é o 12° número primo.
E o inverso deste número, 21, é o resultado da multiplicação de 7 e 3.
Em binário, 73 é um palíndromo: 1001001, que ao contrário é: 1001001, ou seja, a mesma coisa.
E também, o 73° dia do ano é o famoso Dia do Pi.
Com o número 73 também dá para fazer uma mágica legalzinha que você pode fazer com os amigos:
Pegue uma sequencia de 8 dígitos, sendo que os 4 primeiros sejam os mesmos que os 4 últimos (até na ordem!), e depois divida por 137. Feito isso, pegue o resultado e divida-o pelos 4 dígitos do número original (tanto faz serem os 4 primeiros ou os 4 últimos, pois são os mesmos). Não importa o número que você escolha, o resultado final sempre será o 73.
Ótima mágica para se fazer com números de telefones. É só pedir para alguém pensar nos 4 últimos dígitos do telefone de quem ela quiser!
Ex: 12451245 / 137 = 90885
90885 / 1245 = 73
73 é o 21° número primo.
O seu inverso, o número 37, é o 12° número primo.
E o inverso deste número, 21, é o resultado da multiplicação de 7 e 3.
Em binário, 73 é um palíndromo: 1001001, que ao contrário é: 1001001, ou seja, a mesma coisa.
E também, o 73° dia do ano é o famoso Dia do Pi.
Com o número 73 também dá para fazer uma mágica legalzinha que você pode fazer com os amigos:
Pegue uma sequencia de 8 dígitos, sendo que os 4 primeiros sejam os mesmos que os 4 últimos (até na ordem!), e depois divida por 137. Feito isso, pegue o resultado e divida-o pelos 4 dígitos do número original (tanto faz serem os 4 primeiros ou os 4 últimos, pois são os mesmos). Não importa o número que você escolha, o resultado final sempre será o 73.
Ótima mágica para se fazer com números de telefones. É só pedir para alguém pensar nos 4 últimos dígitos do telefone de quem ela quiser!
Ex: 12451245 / 137 = 90885
90885 / 1245 = 73
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Leonhard Euler e a prova da existência de deus
O ateu Denis Diderot andava a ''pregar'' o ateísmo, enchendo o saco de todos na corte de Catarina, a Grande, quando a czarina teve a brilhante ideia de pedir a ajuda do grande matemático Leonhard Euler, que se encontrava também na capital russa.
A ideia era a de que o matemático bolasse uma ''prova'' da existência divina a fim de calar a boca do ateu chato.
Lançado o desafio, assim que Diderot compareceu, esperançoso pra refutar a famigerada ''prova'', eis que Euler anuncia, na frente de todos, assim:
Claro que Diderot não entendeu bulhufas! Humilhado, ele abandona o desafio, para o deleite de Catarina e sua corte!
O ateu Denis Diderot andava a ''pregar'' o ateísmo, enchendo o saco de todos na corte de Catarina, a Grande, quando a czarina teve a brilhante ideia de pedir a ajuda do grande matemático Leonhard Euler, que se encontrava também na capital russa.
A ideia era a de que o matemático bolasse uma ''prova'' da existência divina a fim de calar a boca do ateu chato.
Lançado o desafio, assim que Diderot compareceu, esperançoso pra refutar a famigerada ''prova'', eis que Euler anuncia, na frente de todos, assim:
Cavalheiro, (a+b^n)/n=X, portanto, Deus existe. Responda!
Claro que Diderot não entendeu bulhufas! Humilhado, ele abandona o desafio, para o deleite de Catarina e sua corte!
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Os Sólidos Platônicos
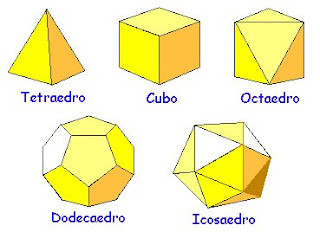
Os Sólidos Platônicos são assim chamados devido a uma homenagem de Euclides em seu livro, Elementos. Ele acreditava que o filósofo Platão foi o primeiro a descrever os cinco poliedros regulares convexos em seu diálogo, o Timeu. Como Platão, e também os gregos antigos, acreditavam que o mundo havia sido criado pelos elementos ar, água, terra e fogo, o filósofo tratou de relacionar cada poliedro a um desses elementos. Para ele, essas figuras geométricas representavam a harmonia e a perfeição do mundo. Portanto, elas tinham que estar relacionadas com os elementos que o criaram.
Mas como, se os sólidos são cinco e os elementos são quatro?
Depois que Platão considerou os únicos poliedros regulares possíveis, que são o Cubo, o Tetraedro, o Dodecaedro, o Icosaedro e o Octaedro, ele teorizou que o elemento Terra estaria ligado ao Cubo, o Fogo ao Tetraedro, a Água ao Icosaedro e o Ar ao Octaedro. É como se os átomos de cada elemento assumissem o formato dessas figuras geométricas. Quanto ao dodecaedro, este seria associado à quintessência, ou a essência do Universo, que Platão chamava de O Cosmos, ou a Alma do Mundo.
Ainda é importante destacar que a descrição dos sólidos feita por Platão deslumbrou grandes cientistas, como Johannes Kepler, que chegou a elaborar um modelo geométrico do sistema solar através dos Sólidos Platônicos, e Leonardo da Vinci, que foi inspirado por eles quando desenhou projetos arquitetônicos.

Os Sólidos Platônicos são assim chamados devido a uma homenagem de Euclides em seu livro, Elementos. Ele acreditava que o filósofo Platão foi o primeiro a descrever os cinco poliedros regulares convexos em seu diálogo, o Timeu. Como Platão, e também os gregos antigos, acreditavam que o mundo havia sido criado pelos elementos ar, água, terra e fogo, o filósofo tratou de relacionar cada poliedro a um desses elementos. Para ele, essas figuras geométricas representavam a harmonia e a perfeição do mundo. Portanto, elas tinham que estar relacionadas com os elementos que o criaram.
Mas como, se os sólidos são cinco e os elementos são quatro?
Depois que Platão considerou os únicos poliedros regulares possíveis, que são o Cubo, o Tetraedro, o Dodecaedro, o Icosaedro e o Octaedro, ele teorizou que o elemento Terra estaria ligado ao Cubo, o Fogo ao Tetraedro, a Água ao Icosaedro e o Ar ao Octaedro. É como se os átomos de cada elemento assumissem o formato dessas figuras geométricas. Quanto ao dodecaedro, este seria associado à quintessência, ou a essência do Universo, que Platão chamava de O Cosmos, ou a Alma do Mundo.
Ainda é importante destacar que a descrição dos sólidos feita por Platão deslumbrou grandes cientistas, como Johannes Kepler, que chegou a elaborar um modelo geométrico do sistema solar através dos Sólidos Platônicos, e Leonardo da Vinci, que foi inspirado por eles quando desenhou projetos arquitetônicos.
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
O matemático britânico G. H. Hardy, quando visitou o gênio hindu da matemática, Srinivasa Ramanujan, disse a ele que havia chegado num táxi cuja chapa continha um número deveras insignificante, 1729.
''Na verdade é um número bem interessante!'', observou Ramanujan. ''É o menor número inteiro que pode ser expresso como a soma de dois cubos, de dois modos diferentes.'' E ele estava certo! Pois:
1729 = 13 + 123 = 93 + 103
Última edição por Alquimista em 30/7/2017, 03:19, editado 3 vez(es)
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Uma questão relacionada à Raiz Quadrada de 2:
Uma vez propus essa questão no blog do Criaturo...
Era sobre um amigo que tive, que brigou comigo numa discussão boba sobre a infinitude dos decimais dos números irracionais e transcendentais.
O motivo da briga: o maluco afirmou que a quantidade de dígitos da raiz quadrada de dois tinha que ser FINITA só porque a medida dela podia ser expressa num quadro-negro como um tracinho bem definido contendo começo e fim, ou seja, só porque tinha ''comprimento finito e definido''!!!!!!!!!!
Ou seja, por que a raiz quadrada de 2 não pode ser irracional só porque é possível traçar sua ''medida'' com um tracinho que tem início e FIM?
PS: não vale citar a prova de Euclides.
Vamos analisar algumas respostas que foram dadas ao desafio dO ALQUIMISTA:
Cientista escreveu:
Esse é um problema linguístico! Em matemática, os números são nomes para quantidades. Cada quantidade tem um nome particular. O problema da representação linguística da realidade é que as palavras falham em representá-la. Não há diferença no caso dos números, que são meras palavras para falar de coisas (quantidades). Duas deturpações linguísticas fundamentais que se encontram em pensamento matemático se expõem nos “conceitos” (ideias/idealizações) de ‘infinito’ e ‘contínuo’, muito interrelacionados. Essas deturpações extrapolam degenerativamente o número de palavras representacionais, tornando-as como que ‘células cancerígenas’ do ‘tecido matemático’. É dessa deturpação filosófico-matemática que surgem quimeras como os ‘números irracionais’
Uma representação geometrizada de uma quantidade encontra um paralelo somatório com representação numérica, isto é, podemos somar comprimentos tanto quanto e conforme somamos números. Tá entendendim?!… Até aquizim?!
É muito simplim facim! É só tu botazim tico e teco pra funcionazim que tu coseguizim, fiim!!! hahahahahahahahahaha… MESTRE tem que falar assim porque é ridículo explicar tal banalidade… hahahahahahahahahahaha…
Se temos um comprimento de um centimetrim, podemos somar a ele, geometricamente, 0,4 centimetrim, resultando 1,4 centimetrim. A esse segmentim, podemos somar 0,01 centimetrim, obtendo 1,41. Tá entendendim?!
Como podes notarzim, cada algarismo mais significativo estabelece um limiar intransponível para a quantidade, prescindindo-se, nessa óbvia verificação direta, de qualquer racionalização mais “profunda” de quimerinhas como ‘limite (de)’. Não importa quantas partes decimais se acumulem, a soma não chegará sequer a 1,42 a partir daquele ponto em que parei. E… hahahahahahahaha… o mesmíssimo óbvio vale para a… correspondente sominha geométrica!!! De pedacinhos cada vez menores alinhados um após outro.
KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK...
mestrim é mesmo o reizim das filosofadas de filoSOF(R)I(D)A(S)!!!!!!!!!
KAKAKAKAKAKAKAKAKAKAKAKAKAKAKAKAKAKA...
Como é que é???!!! Tipo assim, aquele problemim do SEINÃO de Eléia é o que o mestrim filosoFIM di butiquim tem na buquim???!!! NOOOOOOSSA!!!!!!!!!!
HAHAHAHAHAHAAHAHAHAHAHAAHAHAHAHAHAHA...
A propósito, apresentei essas suas patacadas aí no dia da briguinha. Mesmo assim, o maluco não ficou satisfeito.
Para ficar mais claro, o que ele alegava era como que a diagonal de um quadrado cujos lados são 1 pode ser representada por um número cujos decimais nunca terminam??? Segundo ele, os decimais correspondentes à tal diagonal, justamente por ser a diagonal de um quadrado unitário, INSERIDA NELE, deveriam se encerrar em algum número.
É praticamente o mesmo dilema que os pitagóricos enfrentaram quando da descoberta da raiz quadrada de dois. Dizem até que o seu descobridor, membro da ordem pitagórica, foi condenado à morte por abalar a ordem sagrada dos números, segundo as crenças dele, cuja base filosófica era a unidade.
Mas vamos à solução:
Conforme foi demonstrado pela primeira vez por Descartes, toda equação quadrática pode ser resolvida por método geométrico, com simples uso de régua e compasso.
Já qualquer irracional quadrático, por sua vez, pode ser expresso como solução de uma equação quadrática.
Logo é possível expressar precisamente o comprimento de qualquer medida denotada por um número irracional quadrático. ( Se desprezarmos os inevitáveis erros instrumentais inerentes ao processo ).
Bom, é claro que, definida uma unidade básica qualquer de medida de comprimento, estes não seriam os únicos números que poderiam ter sua identificação geométrica precisamente determinada utilizando apenas instrumentos como régua e compasso. Porém esses detalhes insignificantes geralmente não são obstáculos intransponíveis para o entendimento em pessoas consideradas como de inteligência pelo menos normal.
Já para os inferiormente fora da curva tudo demanda um pouco mais de trabalho.
Também é verdade que qualquer número irracional pode ser aproximado até o limite de qualquer erro arbitrariamente estipulado, no pior dos casos, por uma expansão por, assim chamadas, frações contínuas. Sendo que para apenas os quadráticos irracionais é possível aproxima-los por frações contínuas que são periodicamente contínuas.
Perfeito! Mas embora não sejam bobagens como as que o Cientista aqui lamentavelmente despejou, também não resolve o problema do meu amigo.
Porque o problema, e isto está muito claramente explicado, é que ele está realizando um salto no vazio em seu raciocínio lógico. Ele acha que, por toda medida ter comprimento finito, então isso implicaria necessariamente que a representação numérica de toda medida também teria que ser finita.
Então o exato problema que se propõe é como explicar a ESTA pessoa que ele está errado.
Não um tipo de explicação que satisfaça a um Euler. Mas para alguém que sequer compreende o conceito de números irracionais. Muito menos irracionais quadráticos, expansão em frações contínuas, etc…
De forma que um ponto de partida poderia ser demonstrar que qualquer número que possa ser expresso em forma finita ( com um número finito de dígitos ), necessariamente, é um número que pertence ao conjunto dos Racionais.
E mesmo dízimas periódicas também pertencem ao conjunto dos Racionais.
Para isso basta mostrar que em ambos os casos sempre é possível escrever tal número na forma de uma razão de inteiros.
Para o 1° caso se torna trivial: se r tem N dígitos nas casas decimais basta reescrever r como [r*(10^N)] / (10^N)
No 2° bastaria expressar a parte periódica como a soma dos termos de uma PG infinita.
Agora nós poderíamos mostrar a esta pessoa que um segmento de reta poderia ser definido como o traço que é descrito por um ponto que se move por uma determinada distância, sempre na mesma direção. E, no seu movimento entre o ponto inicial A e o ponto final B, passa por todos os infinitos pontos do espaço entre estes dados dois pontos. De forma que, axiomaticamente, um segmento de reta é formado por um conjunto infinito de pontos, sendo que cada um destes tem uma única medida de sua distância ao ponto inicial A.
Então suponhamos um segmento AB de comprimento 1; o sujeito sabe que entre 0 e 1 existem INFINITOS números racionais, ou como ele articula, “infinitos números que podem ser escritos com um número finito de dígitos” . Mas ele também entende que entre A e B existem da mesma forma infinitos pontos.
O que ele precisamente NÃO entende é COMO estes infinitos valores racionais não são suficientes para referenciar cada um dos infinitos pontos no intervalo!
Mas como cada número real entre 0 e 1 pode ser associado a um e apenas um ponto P do segmento AB, podendo ser interpretado como a medida de AP, segue que é suficiente demonstrar que a cardinalidade de ]0,1[ é maior que a cardinalidade de Q.
E portanto não é possível uma função bijetora entre cada ponto no intervalo AB e o conjunto Q. ( Conjunto dos Racionais )
Mas a função f(x)= 1/2 * { [ x / ( 1 + MOD(x) ) ] + 1 } é exemplo de uma bijeção entre o Conjunto dos números Reais e o intervalo ]0,1[
Portanto a cardinalidade do conjunto ]0,1[ é a mesma de R. Sendo que tanto o conjunto dos Racionais quanto dos Irracionais são subconjuntos de R.
A partir de dois famosos teoremas de Cantor demonstramos que Q é infinito enumerável mas R é infinito não enumerável, logo a cardinalidade de R é maior que a de Q. Implicando que cardinalidade de ]0,1[ é também maior que cardinalidade de Q.
Portanto é impossível existir função bijetora entre Q e o conjunto de todos os pontos no intervalo AB.
Daí se conclui que o conjunto dos números racionais (que inclui todos os números que podem ser escritos com um número finito de dígitos) não é suficiente para referenciar todos os pontos do intervalo AB. Logo, existem pontos (medidas, comprimentos de subintervalos em AB) que são expressos por números que não podem ser representados por qualquer número finito de dígitos.
Contrariamente ao que o “tal sujeito” estaria afirmando. É simples assim.
Última edição por Alquimista em 11/5/2018, 00:22, editado 4 vez(es)
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Ilusionismo Matemático
Como só O GRANDE MAGO ALQUIMISTA é capaz de fazer!!!!!!!
O Pedro Reis desafiou:
Pedro Reis escreveu:A título de exemplo apresento a minha proposição, destinada a testar as habilidades algébricas de qualquer um que alegue ser da mais relevante importância a rigorosa algebrização de um problema.
Ei-la:
Demonstre que Somatório de i=1 até N de ( N! / {( N-i )! * i!} ) * (2^i) = (3^N) – 1
N=1
( 1! / {( 1-1 )! * 1!} ) * (2^1) = (3^1) – 1 = 2
N=2
[( 2! / {( 2-1 )! * 1!} ) * (2^1)] + [( 2! / {( 2-2 )! * 2!} ) * (2^2)] = (3^2) – 1 = 8
N=3
[( 3! / {( 3-1 )! * 1!} ) * (2^1)] + [( 3! / {( 3-2 )! * 2!} ) * (2^2)] + [( 3! / {( 3-3 )! * 3!} ) * (2^3)] = (3^3) – 1 = 26
Demonstrada esta identidade eu mostro como isto se relaciona com um método original para maximizar a simplificação de um circuito digital com N entradas e uma saída.
https://religiaodeuslivre.wordpress.com/2016/08/02/topico-dos-desafios-charadas-e-pegadinhas/#comment-1914
E O MESTRE ALQUIMISTA respondeu:
Alquimista escreveu:N=n
n! / {(n-1)! 1!}2^1 + n! / {(n-2)! 2!}2^2 + n! / {(n-3)! 3!2^3 + … + n! / {(n-n)! n!}2^n = 3^n – 1
{n(n-1)! / (n-1)! 1!}2^1 + {n(n-1)(n-2)! / (n-2)! 2!}2^2 + {n(n-1)(n-2)(n-3)! / (n-3)! 3!}*2^3 + … + 2^n = 3^n – 1
n{2^1 / 1! + (n-1)2^2 / 2! + (n-1)(n-2)2^3 / 3! + …} + 2^n = 3^n -1
{2^1 / 1! + (n-1)2^2 / 2! + (n-1)(n-2)2^3 / 3! + …} = (3^n – 2^n – 1) / n
Logo,
n{(3^n – 2^n – 1) / n} + 2^n = 3^n – 1
3^n – 2^n – 1 = 3^n – 2^n – 1
https://religiaodeuslivre.wordpress.com/2016/08/02/topico-dos-desafios-charadas-e-pegadinhas/#comment-1949
BRILHANTE!!!!!!!
Vamos ver como o Pedro Reis reagiu:
Pedro Reis escreveu:Dou nota 11 para a sua solução!
Se tivesse acertado daria 10.
Mas esse “embromation” foi melhor ainda.
KKKKKKKKKKKKKKKKKKK!
Matemágica! Alquimio usando todas as suas habilidades ilusionistas.
A identidade abaixo está correta.
{2^1 / 1! + (n-1)2^2 / 2! + (n-1)(n-2)2^3 / 3! + …} = (3^n – 2^n – 1) / n
Mas depois disso você fez o truque do desaparecimento do lado esquerdo e
demonstrou que o lado direito é igual a… ELE MESMO!
Hahahahahahahahaha!
Rolando Lero não teria feito melhor.
Cara… eu nunca tinha pensado nisso… é uma ideia maravilhosa pra fazer prova em quase todas as cadeiras… cê vai enrolando, enrolando… quando o cara cansar e achar que você sabe o que tá fazendo… pimba!, pula direto pra resposta!
KKKKKKK!!!
E pensar que errei essa no concurso pra gari… Se eu soubesse essa malandragem…
Nota 11.
https://religiaodeuslivre.wordpress.com/2016/08/02/topico-dos-desafios-charadas-e-pegadinhas/#comment-1953
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Mais curiosidades matemáticas interessantes:
O mistério dos Quadrados Mágicos:
https://mestredoconhecimento.forumeiros.com/t8-grandes-misterios-da-humanidade-finalmente-desvendados-pelo-alquimista#49
26 é o único número que está situado exatamente entre um quadrado (25) e um cubo (27).
Confiram o super enigma que bolei utilizando essa curiosidade:
https://mestredoconhecimento.forumeiros.com/t14-invencoes-verdadeiramente-geniais#118
Última edição por Alquimista em 22/4/2018, 18:56, editado 5 vez(es)
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
O ''passeio do cavalo'' do Xadrez:
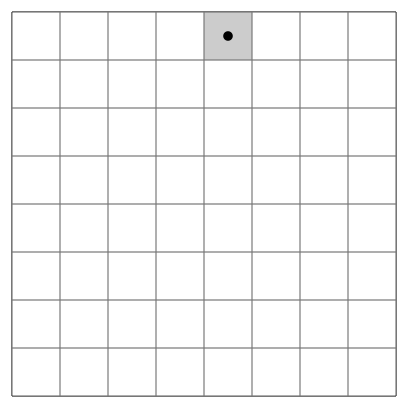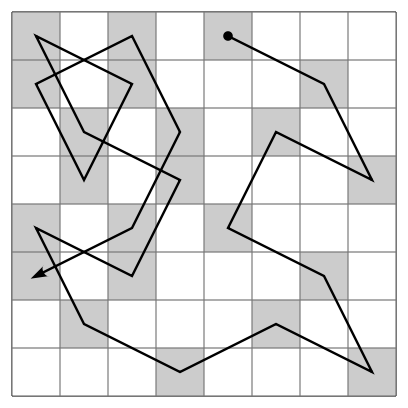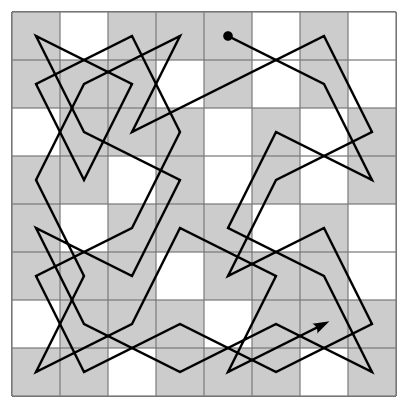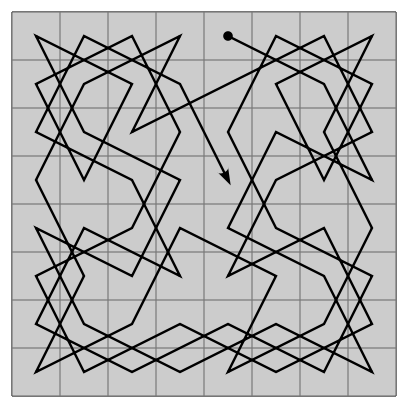
Este é um problema muito antigo, que consiste em descobrir uma sequência de passos para o cavalo, de modo a fazê-lo visitar todas as 64 casas do tabuleiro de xadrez, sem passar pela mesma casa duas vezes. Este problema já era estudado pelos Árabes, mas nos últimos séculos foi resolvido por vários matemáticos. Em 1720, o matemático Brook Taylor (1685-1731) reaviva o problema, mas o mérito para a descoberta da primeira solução pertence a De Moivre (1667-1754). Rapidamente outras soluções apareceram, mas é a De Moivre que se costuma atribuir o crédito da primeira solução publicada. Apresento agora quatro soluções para este problema, sendo as três primeiras da autoria dos matemáticos De Moivre, Montmort, Mairan, e a última, feita por um computador através de um método CSA ("Computer Simulated Annealing"). Estão desenhados sobre os tabuleiros os percursos que passam pelas 64 casas. Para percorrer um passeio inteiro, começa-se pela casa com o número "1" e progride-se até à casa marcada com o número "64".


Comparando estas quatro soluções, vemos claramente que as que foram obtidas pelos matemáticos são bastante mais regulares que a solução pelo método CSA. Muito sucintamente, este método, claramente só concretizável através de um computador, consiste em definir uma sequência aleatória com os números das 64 casas. Sempre que duas casas consecutivas na sequência estão separadas no tabuleiro por uma distância cujo quadrado é cinco (ou seja, casas que distem uma da outra de um salto do cavalo), a "energia" desse par é feita nula. A "energia" não passa, no fundo, de uma função de custo, que serve para medir a qualidade de uma sequência, e deseja-se que o valor desta função de custo seja tão baixo quanto possível. Casas consecutivas na sequência que não distem de um salto do cavalo recebem um valor energético positivo qualquer. Depois, o computador troca os pares de casas entre si (claro, apenas os que ainda não distam de um salto do cavalo), até atingir uma sequência de passos cuja energia total dê zero. Então ter-se-á atingido uma solução para o problema pois todas as 64 casas consecutivas na sequência distarão de um salto do cavalo.
A mente humana usa, obviamente, métodos bem diferentes para resolver o problema. Tipicamente, tenta-se primeiro dividir o tabuleiro em duas regiões que possam ser resolvidas separadamente. Observando as soluções feitas pelos matemáticos é fácil constatar que eles usaram métodos bem claros: Monmort preferiu dividir o tabuleiro em duas metades, resolvendo cada uma separadamente; Mairan e De Moivre preferiram fazer a separação entre a periferia do tabuleiro e o seu centro. Claramente, a solução CSA contrasta das primeiras por não revelar qualquer padrão ou estrutura regular.
Será fácil concordar com o fato de que a solução de De Moivre é a mais elegante das quatro apresentadas. De Moivre separa claramente o percurso na periferia iniciado no canto superior direito com o fim do "passeio", quando se entra na zona central. Como é evidente que não se pode fazer um passeio num quadrado de lado quatro, é de esperar que De Moivre tivesse que usar duas casas da região central para o seu percurso periférico. Simplesmente não se pode fazer um passeio que use todo o anel periférico de 48 casas e que depois passe à região central de 16 casas. Assim, a escolha das duas casas da região central que irão ser usadas no percurso na periferia constitui um grau liberdade que leva a que exista uma quantidade razoável de soluções parecidas com a de De Moivre.
Já a solução cíclica é a que há reentrância, ou seja, da casa 64 pode-se saltar por um movimento do cavalo para a casa 1 e recomeçar o passeio de novo. Apenas ficamos com uma solução mais elegante!
As regras criadas por Euler (1707-1783) em 1759, permitem facilmente alterar a solução de De Moivre de modo a obter uma solução cíclica. Como exemplo, veja-se na figura uma variante da solução de De Moivre tornada cíclica, ou reentrante, pelas regras de Euler:

Fonte: http://bmotta.planetaclix.pt/rennes_intro.html?pergaminhos2.html
Eis a solução fechada feita pelo célebre autômato jogador de xadrez, O Turco:

 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Lei de formação do CPF:
d1d2d3.d4d5d6.d7d8d9-d10d11 (d10, d11 = dígitos de controle)
Os dígitos d1, d2, ..., d8, d9 são escolhidos aleatoriamente. Os dígitos de controle são calculados como segue:
1° Dígito:
Soma = 1×d1 + 2×d2 + 3×d3 + 4×d4 + 5×d5 + 6×d6 + 7×d7 + 8×d8 + 9×d9 =
Resto = Soma mod 11
≤ 9 → d10 = Resto
> 9 → d10 = 0
2° Dígito:
Soma = 0×1d + 1×2d + 2×3d + 3×4d + 4×5d + 5×d6 + 6×d7 + 7×d8 + 8×d9 + 9×d10 =
Resto = Soma mod 11
≤ 9 → d11 = Resto
> 9 → d11 = 0
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Suponha que um ente vive no espaço R (espaço unidimensional), ou seja, numa reta.
Então, um ponto desta reta seria um obstáculo. Para que o ente ultrapasse este ponto, ele teria que avançar uma dimensão, isto é, entrar no espaço R2 (espaço bidimensional), que é um sistema de eixos cartesianos ortogonais.
Assim, o ente pode transitar pelo espaço R×R até encontrar o seu novo obstáculo, que no espaço R2 é uma reta.
Para ultrapassar esta reta, este ente teria que avançar mais uma dimensão, ou seja, entrar no espaço R3 (espaço tridimensional), que é um sistema de três eixos ortogonais.
Então o ente poderá transitar pelo espaço R×R×R até encontrar o obstáculo do espaço R3, que é um plano.
Para atravessar planos, como paredes e muros, só bastaria entrar no espaço R4 (espaço quadridimensional, ou hiperespaço).
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Representação de números por frações contínuas:
√2 = 1 + 1
2 + 1
2 + 1
2 + 1
2 + ...
1 ano ≈ 365 + 1 ou, mais resumidamente, 1 ano ≈ 365 + 1/4 dias.
4 + 1
7 + 1
1 + 1
3 + ... dias
Número áureo: φ = 1 + 1 ou, φ = 1,618...
1 + 1
1 + 1
1 + 1
1 + ...
√29 = 5 + 1
2 + 1
1 + 1
1 + 1
2 + 1
10 + 1
2 + 1
2 + 1
2 + ...
Número neperiano: ℮ = 2 + 1
1 + 1
2 + 1
1 + 1
1 + 1
4 + 1
1 + 1
1 + 1
6 + 1
1 + ...
Número pi: π = 3 + 1
7 + 1
15 + 1
1 + 1
292 + ...
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Poucos sabem que a relação entre a matemática e música está bem longe de ser desimportante. Música é matemática. E a música grega, que serviu de base para o desenvolvimento da música ocidental, surgiu das mãos dos matemáticos gregos. Todos já devem ter ouvido falar da "música das esferas", de Pitágoras, que consiste na ressonância harmônica existente entre o movimento de rotação dos astros e as formas universais que configuram a natureza. Incluindo-se aqui o som. Existe também no diálogo "O Timeu", de Platão, interessante discussão sobre o assunto.
Outra coisa que também muitos não sabem é que Bach foi tremendo matemático (amador) e que algumas peças dele têm uma concepção completamente numérica. O lirismo é ulterior, racionalidade a serviço do belo.
O prelúdio 1 do Cravo Bem Temperado é um quadrado mágico de 6, tirando-se o ápice da tensão - se não engano fica no compasso 28 e tem disposição espacial advinda de cálculo de proporção com o número áureo - e incidindo-se no coda, todas as seções ficam muito bem divididas de modo a elucidar os espaçamentos "sentimentais", subordinando-os ao cálculo que concebeu sua alocação.
E também compositores da envergadura de um Xenákis já reincidem na verve matemática, como no estudo das probabilidades em ordenação de sistemas.
A discussão neste campo é muito rica.
sombriobyte- Mensagens : 602
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Bach ainda trabalhou muito com simetrias, umas espécies de espelhos alternados, das linhas de solo com a do acompanhamento. Bach é realmente apaixonante, muito criativo.
Umas das relações mais interessantes são as notas musicais, elas são vibrações, que podem ser medidas por um números determinados, que sobem ou descem, como se cada nota compreendesse uma quantidade x de passos...
O surgimento das escalas pentatônicas, em lugares diferentes, da mesma forma... é muito assunto...
sombriobyte- Mensagens : 602
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Sempre achei que o fato das escalas pentatônicas terem surgido em lugares os mais diversos se devesse à causas de organização social. Mas por que não poderia tal forma de organização seguir padrões matemáticos?
Não sei se vocês conhecem a teoria dos fractais, que fala da recuperação do todo nas partes de um sistema geométrico pré definido com ordenação na falta de padrão? Então, esta é uma ideia que serve de inspiração para mecanismos de organização composicional. O fato do nariz do árabe parecer com sua espada, que por si parecem mutuamente com as corcovas de um camelo, são um sintoma de que a natureza adota padrões geométricos em categorias de objetos aparentemente distantes.
O termo correto para isso seria citar uma "plurivocidade cosmética" dentro de um conjunto de possibilidades pré estabelecidas por uma limitação em matéria de forma.
Por esse motivo pode-se extrair substratos tão diferentes da forma-sonata, sem que se perca o sustentáculo, ou analisar a origem de uma escala numa sociedade olhando para os aspectos biológicos, sociais, psíquicos e matemáticos - que podem fazer do vir-a-ser materializado numa escala um desmembramento de possibilidades inerentes à forma que deu origem ao(s) conteúdo(s), pois pelo que me parece, as hexatônicas não distam muito em termos de organização social, o imobilismo, a figura recorrente, etc...
E até mesmo os intervalos - a despeito de uma suposta sociabilidade da formação das escalas - são matemáticos, pois se definem como diferenciação de proporções numéricas.
sombriobyte- Mensagens : 602
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Além disso, as relações da física com a música são também deveras capciosas. A criação dos instrumentos, por exemplo, a harpa baseia-se na possibilidade de extrair-se sons cada vez mais agudos de acordo com o encurtamento da corda dedilhada. Por isso que o piano de cauda tem aquele formato. Isso aí se chama logaritmo, e sua relação com a escala cromática, que é um logaritmo de base 2. Incrível não é? - longa vida à interdisciplinaridade!
Auf wiedersehen
sombriobyte- Mensagens : 602
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Sombriobyte:
Fractais, um conceito desconhecido a priori devido à sua conotação matemática, porém mais próximo do nosso ambiente do que pensamos. Os Fractais, descobertos pelo matemático polaco Benoît Mandelbrot, definem-se como figuras planas ou espaciais, compostas de elementos infinitos, que têm a propriedade de ter um aspecto e distribuição estatística que não mudam seja qual for a escala que se observe.
Na natureza encontramos uma infinidade de exemplos, como os flocos de neve, as nuvens, os neurônios ou uma simples couve-flor.
A ciência dos fractais apresenta estruturas geométricas de grande complexidade e beleza infinita, ligadas às formas da natureza, ao desenvolvimento da vida e à própria compreensão do universo. São imagens de objetos abstratos que possuem o caráter de onipresença por terem as características do todo infinitamente multiplicadas dentro de cada parte, escapando assim, da compreensão em sua totalidade pela mente humana.

Bibi- Mensagens : 198
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
A teoria do caos é um ramo matemático que se ocupa dos sistemas que apresentam um comportamento imprevisível aparentemente aleatório, embora regidos por leis estritamente deterministas. Isso se deve ao fato de as equações não lineares que regem a evolução desses sistemas serem muito sensíveis a variações em suas condições iniciais. Assim, uma pequena alteração no valor de um parâmetro pode gerar grandes mudanças no estado à medida que o sistema evolui. Sabe aquele exemplo do sistema borboleta? Muitas vezes porém dentro desse sistema caótico pode aparecer um padrão. A esse padrão dentro do caos é que se deu o nome de fractal.
Na teoria do caos tem um padrão que é chamado de atrator (Mandelbrot iniciou o estudo dos fractais baseado em objetos caóticos como por exemplo o Conjunto de Cantor e a Função de Weiertrass que é objeto de início do estudo sobre o caos), que PODE ser explicado por fractais. Essas teorias surgiram independentemente uma da outra. E em domínios diferentes, sendo a do CAOS mais para mecânica e estatística e os Fractais da geometria.
Se tivermos em conta que dinâmico implica não constante e não periódico (como o Atractor de Lorenz), podemos dizer que a Teoria do Caos estuda sistemas dinâmicos não-lineares ou, de uma forma mais simples, sistemas deterministas (regidos por leis exatas), cuja elevada sensibilidade às condições iniciais origina resultados aparentemente aleatórios. E a ''linguagem do Caos'' é a própria geometria fractal: só esta permite a irregularidade infinitesimal e só esta nos dá a noção de que uma perturbação numa escala microscópica pode estar associada a uma perturbação de enormes proporções, através das ideias de escala e padrão; enfim, só esta permite descrever um Universo que é bastante mais rico do que a Geometria de Euclides pode conceber.

Bibi- Mensagens : 198
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Perguntas Básicas!
Sou novato nessa história toda... Então, lá vai!
1ª pergunta: Qual a relação entre os fractais e a Teoria do Caos?
2ª pergunta: Qualquer equação (tipo "ax²+bx+c=0") gera um fractal?
3ª pergunta: Quais os melhores programas para gerar fractais?
4ª pergunta: Quem realmente descobriu os fractais? Udo de Aachen ou Benoit Mandelbrot?
5ª pergunta: Quais os fractais que mais ocorrem na natureza?
6ª pergunta: O que são números complexos?
7ª pergunta: Quem é a Júlia (do conjunto)?
8ª pergunta: Qual a relação entre os fractais e o plano cartesiano?
Acho que por enquanto deu...

Agradeço desde já.

Flautista de Hamelin- Mensagens : 252
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
A 1ª pergunta: Qual a relação entre os fractais e a Teoria do Caos?
A Teoria do Caos estuda sistemas dinâmicos não lineares, ou seja, aqueles onde a resposta do sistema a certa interferência não pode ser prevista a partir do comportamento de seus elementos constituintes, é onde a espontaneidade surge na natureza... nossa mente, o clima e a dinâmica de um sistema gravitacional com 3 corpos ou mais.
Fractais aparecem na Teoria do Caos como os atratores desse sistema, ou seja, gráficos que retratam o comportamento desse sistema quando o tempo é usado como parâmetro.
A 2ª pergunta: Qualquer equação (tipo "ax²+bx+c=0") gera um fractal?
Não, equações recursivas, mesmo as mais simples, geram fractais.
Você poderia dizer: z_n+1=(z_n)^2+c, que gera fractais... você começa com z_0=0, por exemplo, escolhe qualquer valor no plano complexo como um c e passa a calcular, z_1 vai ter o valor de c, z_2 de (z_1)^2+c=c^2+c e vai repetindo essa aplicação.
A 3ª pergunta: Quais os melhores programas para gerar fractais?
Apophis, imagino.
A 4ª pergunta: Quem realmente descobriu os fractais? Udo de Aachen ou Benoit Mandelbrot?
Mandelbrot fez um trabalho espetacular, nem conheço o tal Udo.
A 5ª pergunta: Quais os fractais que mais ocorrem na natureza?
Provavelmente aqueles que envolvem a proporção áurea, como a espiral logarítmica..
A 6ª pergunta: O que são números complexos?
São números que possuem parte real e parte imaginaria, da forma a+bi, onde a e b são reais, e i = raiz quadrada de menos 1.
A 7ª pergunta: Quem é a Júlia (do conjunto)?
Gaston Julia, um matemático francês famoso, que perdeu o nariz durante a primeira guerra mundial. Ele calculava os pontos do Conjunto de Julia à mão, levava muito tempo...
A 8ª pergunta: Qual a relação entre os fractais e o plano cartesiano?
Fractais geralmente são definidos no plano dos números complexos, uma generalização do plano cartesiano, onde a unidade imaginaria esta definida como raiz de -1.

Bibi- Mensagens : 198
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Os objectos matemáticos fragmentados e irregulares, com estrutura que se repete em escalas distintas, foram descritos em 1975 como fractais. O autor foi Benoît Mandelbrot, o matemático franco-americano que faleceu em 2010, aos 85 anos, de um cancro no pâncreas.
Nascido na Polónia, judeu, e emigrado aos 11 anos para Paris, França, em 1936, o matemático estava fixado nos Estados Unidos desde 1958. Fez investigação científica na IBM durante 30 anos. Depois, foi professor na Universidade de Yale até 2005.
A biologia, a física, a astronomia e a economia foram algumas das disciplinas que beneficiaram dos fractais – que se encontram por toda a natureza. São objectos que podem ser infinitos, matematicamente, em que escalas cada vez mais pequenas repetem a geometria da escala maior.
''Se cortarmos um dos ramos da couve-flor, vemos toda a couve-flor, mas mais pequena. Se cortarmos o ramo outra vez, e mais outra, e outra, teremos couves-flores mais pequenas. Portanto, há formas que têm esta peculiar propriedade, em que cada parte é como o todo, mas mais pequena'', aclarou antes de falecer.

Bibi- Mensagens : 198
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Lembro de um livro de física, dizendo que quem calculou as notas musicais foi um grande matemático chamado Johann Sebastian Bach. (risos)
Ele na verdade só pegou a oitava e dividiu em 12 partes "iguais", mas fazendo assim:
inventou um sistema de notas iguais, o sistema temperado.
Há uma constante fundamental, raiz décima segunda de 2. (ou 2 elevado a 1/12, que dá 1,059463). Esse é o intervalo de 1 semitom. Para saber a frequência de um semitom acima de uma nota, basta multiplicar a frequência dessa nota por esta constante; para descobrir a frequência de um semitom abaixo, vc pega a frequência e divide.
Por exemplo:
Lá = 440 Hz
Lá# = 440 * ( 2^(1/12) ) = 440 * 1,059463 = 466,2 Hz
Lá b = 440 / ( 2^(1/12) ) = 440 / 1,059463 = 415,3 Hz
Para calcular intervalos maiores, basta ir multiplicando os semitons, ou se usar a matemática, um intervalo de 2 semitons é igual à constante elevada ao quadrado; ou um intervalo de 5 semitons é a constante elevada a cinco.
Exemplos:
Quero saber a frequência do Dó acima do Lá.
Lá-Lá#-Si-Dó, 3 semitons de intervalo:
Dó = 440 * ( 2^(1/12) ) ^ 3 = 440 * (1,059463 ^ 3) = 523,25 Hz
ou, usando a matemática:
Dó = 440 * ( 2^(3/12) ) = 440 * 1,1892 = 523,25 Hz
Quero saber a frequência do Lá uma oitava acima do Lá 440.
São 12 semitons de intervalo:
Lá = 440 * ( 2^(12/12) ) = 440 * 2 = 880 Hz
É isso!
Tom Severo- Mensagens : 32
 Re: Curiosidades Matemáticas
Re: Curiosidades Matemáticas
Muito bom! Só uma observaçãozinha...
Posso estar enganado, mais quem inventou o sistema temperado não foi Bach. Preciso pesquisar, mas ele foi um dos defensores, não o inventor.
sombriobyte- Mensagens : 602
Página 1 de 7 • 1, 2, 3, 4, 5, 6, 7 
Página 1 de 7
Permissões neste sub-fórum
Não podes responder a tópicos
 Início
Início



